Bonjour!

Je poursuis mon exploration de l'univers des fractales.

Dans mon post précédent, j'ai expliqué comment faire l'hexagone de Sierpinski.

Aujourd'hui, je vous parlerai du flocon de Koch.

 

Le flocon de Koch est fait à partir de la courbe de Koch.

 

Maintenant puisque Blender n'est pas un logiciel spécialisé pour faire des images de fractale,

il faut trouver des astuces pour parvenir à nos fins.

Ainsi pour obtenir un beau flocon de Koch, un bon moyen est de faire l'hexagone de Sierpinski.

 

Où se cache le flocon de Koch dans l'hexagone de Sierpinski?

Bien, le flocon de Koch est tout le contour interne de l'hexagone de Sierpinski.

Voyez l'image ci-dessous.

Mais ce contour est formé à partir des côtés des hexagones.

Par conséquent les vertices de ce contour ne sont pas tous connectés ensemble.

 

Pour faire le flocon de Koch à partir de l'hexagone de Sierpinski il faut suivre cette procédure.

 

01 - Faire un hexagone de Sierpinski sur 4 niveaux de copie.

02 - En Edit Mode (Touche Tab) sélectionner le contour interne de l'hexagone de Sierpinski comme dans l'image ci-dessus.

03 - Faire une copie de la sélection en appuyant sur les touches Shift + D.

 

04 - Rendre la copie indépendante en appuyant sur la touche P puis cliquer sur Selection dans le menu pop-up.

05 - Retourner en Object Mode en appuyant sur la touche Tab.

06 - Sélectionner l'hexagone de Sierpinski et appuyer sur la touche H pour le cacher. (Note : Alt + H pour l'afficher de nouveau)

 

07 - Sélectionner le contour du flocon de Koch.

08 - Appuyer sur la touche Tab pour aller en Edit Mode.

09 - Appuyer sur les touches Ctrl + Tab, puis sur la touche 1 pour passer en Vertex Select Mode.

 

10 - Toutes les pointes ont 2 vertices qui doivent être fusionnés en un seul vertex.

       Appuyer sur la touche C pour appeler l'outil Cercle de sélection et sélectionner les 2 vertices sur le bout d'une pointe.

 

11 - Appuyer sur les touches Alt + M, puis cliquer sur At Center dans le menu.

       Note : On peut aussi faire Alt + M puis appuyer sur la touche 3 ou la touche C

      

12 - Répéter les étapes 10 et 11 pour toutes les pointes autour du flocon.

       De temps à autre appuyer sur la touche L pour vérifier qu'aucune pointe n'a été oublié.

       La touche L permet de sélectionner un objet en entier après qu'on ait sélectionné une partie d'un objet.

       Dans notre cas, il suffit qu'un vertex soit sélectionné, puis on appuie sur la touche L.

       On verra la partie du contour qu'on a terminé comme dans l'image ci-dessous.

      

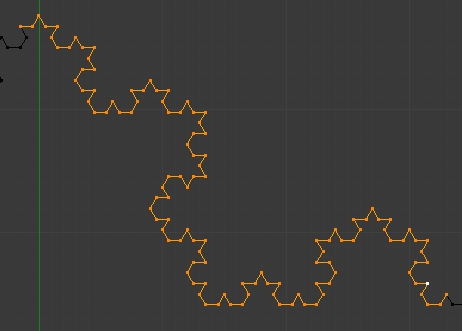
13 - Après avoir fait le tour du flocon, on peut appuyer sur la touche F pour lui faire une face.

 

Maintenant, il ne reste plus qu'à lui mettre une couleur et peut-être aussi une texture.

On peut l'extruder pour faire une colonne. Bref, seul votre imagination limite les possibiltés.

Ci-dessous, un flocon de Koch sert à masquer une partie d'une image : une trace de ski de fond dans la neige.

Pour cela, dans un logiciel comme GIMP ou Photoshop

• Ajouter un canal de transparence au masque
• Sélectionner > par couleur  (Le flocon aura bien sûr une couleur uniforme.)
• Effacer la sélection pour faire le trou du masque.
• L'image sous le masque devient visible uniquement dans la zone qui a été effacé.

 

Noter que sur la page web expliquant la courbe de Koch, on y présente une petite animation qui montre comment

faire le flocon de Koch à partir de plusieurs triangles. 

 

Ci-dessous, l'image montre 2 colonnes et une table faites avec un flocon de Koch que j'ai fait

avec la méthode des triangles. Le flocon dans les airs a été fait à partir de l'hexagone de Sierpinski.

Les 2 colonnes ne sont pas identiques. Pour la colonne du fond, j'avais oublié de mettre quelques triangles.

Mais je l'ai gardé quand même. J'ai coloré le contour de différentes couleurs pour un meilleur relief des colonnes.

 

Ci-dessous, une vue du flocon fait avec la méthode des triangles en Edit Mode.

Ici le fichier blend contenant les 2 versions du flocon de Koch (méthode des triangles, méthode de l'hexagone de Sierpinski).

Voilà! C'est terminé pour le flocon de Koch.

 

Voici 2 liens vers des freewares pour faire des fractales : lien 1 et lien 2.

 

J'expliquerai la fractale de Sierpinski dans mon prochain post pour clore cette série sur les fractales.

 

Mes amis!

Puissent un jour la paix et l'harmonie régnée partout sur la Terre.

À la prochaine!